NP 문제

살면서 여러가지 문제들에 마주치다보면 어떤 것은 매우 쉽고 빠르게 해결할 수 있는 반면에, 해결하기가 매우 어렵고 오래 걸리는 일도 있습니다. 컴퓨터학에서는 문제의 어려움을 계산 복잡도를 사용하여 나타냅니다. 쉽고 빠르게 해결할 수 있는 문제들은 계산 복잡도가 낮다고 하며, 해결하기 어렵고 복잡한 문제일수록 계산 복잡도가 높다고 합니다. 그런데, 어떤 문제들은 적절한 시간 내에 풀 수 있을지 없을지조차 모르는 것들도 있습니다. 다음의 문제를 하나 봅시다.

당신은 휴가를 맞아 여행을 가기로 하였습니다. 비록 휴가는 일주일 밖에 안되지만, 욕심이 많은 당신은 이집트, 스페인, 네덜란드 3개국의 카이로, 알렉산드리아, 바르셀로나, 그라나다, 마드리드, 암스테르담, 헤이그 7개 도시를 방문하려고 합니다. 각 도시들 사이에는 직행 비행기로 이동할 수 있다고 할 때, 쾌적한 여행을 즐길 수 있도록 도시를 중복 방문하는 일 없이 최단 거리 여행 계획을 짜보세요!

당신은 지도를 펴놓고 고민하기 시작합니다. 당신은 한 도시에서 다른 도시로 넘어갈 때 근처에 있는 도시를 먼저 방문하는 것이 최단 경로를 줄이는 방법이라는 것을 알고 있습니다. 따라서 도시들을 어떤 순서로 방문해야 쾌적한 여행을 즐길 수 있는지 그다지 고민하지 않고 결정할 수 있습니다. 하지만 이 문제를 컴퓨터에게 풀게 한다면, 컴퓨터는 한 도시를 방문한 후 어떤 도시를 방문해야 쾌적한 여행이 될지 결정할 수 없습니다. 따라서 도시를 중복 방문하지 않는 수많은 여행 코스¹ 를 모두 비교하여 최단 코스가 무엇인지 찾아내야 할 겁니다.

이와 같이, 어떤 알고리즘을 수행하는데 있어 한 단계에서 다음 단계로 진행할 때 여러 선택권을 가질 수 있는 문제들을 NP (Non-deterministic in Polynomial time) 문제라고 합니다².

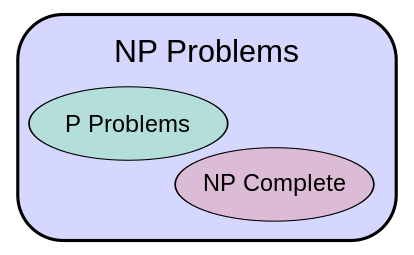
위의 그림처럼, NP 문제는 크게 P 문제와 NP-Complete 문제로 나눌 수 있습니다. P 문제는 결정적인(deterministic) 알고리즘을 사용하여 적절한 시간 (polynomial time) 안에 해결할 수 있는 문제입니다. 반면에 NP-Complete 문제들은 비결정적인(non-deterministic) 알고리즘으로는 적절한 시간 내에 해결할 수 있지만, 결정적인 알고리즘으로는 적절한 시간 안에 해답을 얻을 수 있는 방법을 찾지 못한 문제들 입니다. NP-Compete 문제들의 특징은 해결 방법이 없는 것이 아니라, 해결 방법이 있지만 입력의 크기가 커질수록 계산복잡도가 엄청나게 커진다는 것입니다³. 그래서 NP-Complete 문제들은 보통 다음의 세 접근 방법을 통해 해결합니다.

• Approximate algorithm: 적절한 범위 내에서 차선의(suboptimal) 해결책을 구하는 알고리즘입니다.
• Probabilistic algorithm: 문제의 입력의 확률 분포에 대하여 평균적으로 좋은 성능을 보이는 알고리즘입니다.
• Heuristic algorithm: 대부분의 경우에 잘 동작하지만, 항상 최선의 결과를 얻는다는 보장은 없는 알고리즘입니다.

NP 문제에서 단연 최고의 이슈가 되고 있는 것은 ‘P=NP?’ 입니다. (이 문제는 용의자 X의 헌신에도 나왔었죠.) 즉, ‘NP에 속하는 모든 문제는 결정적인 알고리즘을 사용하여 적절한 시간 내에 해결할 수 있다.’ 라는 명제가 참인지 거짓인지를 판명하는 것입니다. 만약 이 명제가 참이 된다면, 모든 NP-Complete 문제들은 쉽게 해결할 수 있는 방법이 있다는 것이 되므로 엄청난 센세이션을 불러일으키게 되겠죠. 현재는 ‘P 문제는 NP 문제가 될 수 있다.’ 라는 명제가 참이라는 것까지 증명된 상태입니다. (Denis Shasha, 1995)

NP-Complete 문제들은 정말 상당히 흥미로운 것들이 많습니다. 그 중에서도, 그래프는 본연의 구조적 특성 때문에 일반적으로 연산이 굉장히 복잡해서, 상당히 많은 NP-Complete 문제들이 있습니다. 다음엔 그래프에서의 NP-Complete 문제들에 대해 포스팅해보겠습니다.

NP 문제와 관련된 추천 사이트

• Graph of NP-Complete Problems: NP-Complete 문제들을 그래프로 보여줍니다.
• Gödel’s Lost Letter and P=NP: 조지아 텍 교수인 Dick Lipton의 블로그입니다. 알고리즘에 관한 흥미로운 글이 많이 올라옵니다.

1. 7개의 도시를 중복되지 않게 방문하므로, 총 방법의 수는 6! = 720개가 됩니다.
2. NP 문제의 정의는 비결정적인 알고리즘(non-deterministic algorithm)을 사용하여 적절한 시간(polynomial time) 내에 해결이 가능한 문제입니다.
3. 일반적으로 NP-Complete 문제들의 계산복잡도는 sⁿ 에 비례합니다. 여기서 s는 상수, n은 입력의 크기